În acest articol încercăm să înțelegem Legea lui Ohm și Legea lui Kirchhoff prin intermediul formulelor și explicațiilor standard de inginerie și prin aplicarea ecuației diferențiale liniare de ordinul întâi pentru a rezolva exemple de seturi de probleme.

Ce este un circuit electric

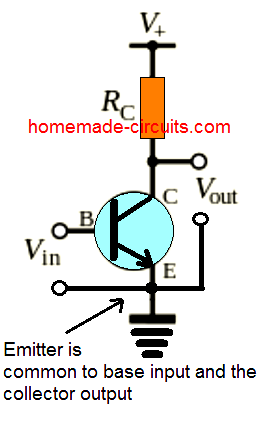
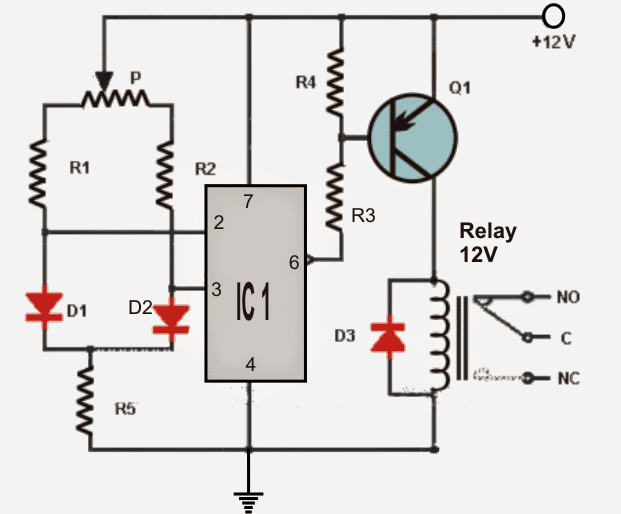
Un circuit electric cel mai simplu este, în general, sub forma unui circuit de serie care are o sursă de energie sau o forță electromotivă, cum ar fi de la o baterie sau un generator de curent continuu, și o sarcină rezistivă care consumă această energie, de exemplu un bec electric, așa cum se arată în diagrama de mai jos:

Referindu-ne la diagramă, când comutatorul este închis, curent Eu trece prin rezistor, provocând generarea unei tensiuni peste rezistor. Adică, atunci când sunt măsurate, diferențele de potențial la cele două puncte finale ale rezistorului vor arăta valori diferite. Acest lucru poate fi confirmat folosind un voltmetru.

Din situația explicată mai sus, legea standard a lui Ohm poate fi dedusă ca:

Căderea de tensiune ER pe un rezistor este proporțională cu curentul instantaneu I și poate fi exprimată ca:

ER = RI (Ecuația nr. 1)

În expresia de mai sus, R este definită ca constantă a proporționalității și se numește rezistență a rezistorului.

Aici măsurăm tensiunea ESTE în Volți, rezistența R în Ohms și curentul Eu în amperi.

Aceasta explică legea lui Ohm în forma sa cea mai de bază într-un circuit electric simplu.
În circuitele mai complexe, încă două elemente esențiale sunt incluse sub formă de condensatori și inductori.

Ce este un inductor

Un inductor poate fi definit ca un element care se opune unei schimbări de curent, creând un efect de inerție în fluxul de electricitate, la fel ca o masă în sistemele mecanice. Experimentele au dat următoarele rezultate pentru inductori:

Căderea de tensiune THE într-un inductor este proporțional cu rata instantanee de schimbare a curentului I. Aceasta poate fi exprimată ca:

EL = L dl / dt (Ecuația nr. 2)

unde L devine constanta proporționalității și se numește inductanța inductorului și se măsoară în henrys. Timpul t este dat în secunde.

Ce este un condensator

Un condensator este pur și simplu un dispozitiv care stochează energia electrică. Experimentele ne permit să obținem următoarea explicație:

Căderea de tensiune pe un condensator este proporțională cu sarcina electrică instantanee Q de pe condensator, aceasta poate fi exprimată ca:

EC = 1 / C x Q (Ecuația nr. 3)

unde C este denumit ca capacitate , și se măsoară în farade taxa Î se măsoară în Coulombs.

Cu toate acestea din moment ce IC) = dQ / dt, putem scrie ecuația de mai sus ca:

Valoarea curentului Aceasta) poate fi rezolvat într-un circuit dat prin rezolvarea ecuației produse prin aplicarea următoarei legi fizice:

Înțelegerea legii lui Kirchhoff (KVL)

Gustav Robert Kirchhoff (1824-1887) a fost un fizician german, legile sale populare pot fi înțelese așa cum sunt povestite mai jos:

Legea actuală a lui Kirchhoff (KCL) prevede că:

În orice punct al unui circuit, suma curenților de intrare este egală cu suma curentului de ieșire.

Legea tensiunii Kirchhoff (KVL) prevede că:

Suma algebrică a tuturor căderilor de tensiune instantanee în jurul oricărei bucle închise este zero sau tensiunea imprimată pe o buclă închisă este egală cu suma căderilor de tensiune din restul buclei.

Exemplul nr. 1: Referindu-ne la diagrama RL de mai jos și, combinând ecuația # 1,2 și tensiunea lui Kirchhoff, putem obține următoarea expresie:

Ecuația: 4

Să luăm în considerare acest caz A cu o forță electromotivă constantă:

În ecuația descrisă mai sus # 4 dacă E = E0 = constantă, atunci putem conduce următoarea ecuație:

Ecuația: 5

Aici ultimul termen se apropie de zero ca t tinde să meargă la infinit, astfel încât Aceasta) tinde spre valoarea limitativă E0 / R. După o întârziere suficient de lungă, voi ajunge la o constantă practic, fără a depinde de valoarea lui c, ceea ce implică și faptul că aceasta va fi independentă de o condiție inițială care ar putea fi forțată de noi.

Având în vedere condiția inițială a fi, I (0) = 0, obținem:

“cum se convertește curent alternativ în curent alternativ ”

Ecuație: 5 *

Cazul B (Forța electromotivă periodică):

Luand in considerare E (t) = Eo sin ωt, apoi luând în calcul ecuația # 4, soluția generală pentru cazul B poate fi scrisă ca:
(∝ = R / L)

Integrarea acestuia pe părți ne oferă:

Acest lucru poate fi derivat în continuare ca:
ઠ = arc până ωL / R

Aici termenul exponențial tinde să se apropie de zero, deoarece t tinde să ajungă la infinit. Aceasta implică faptul că, odată ce a trecut o perioadă de timp adecvată, curentul I (t) atinge o oscilație practic armonică.